Support the standard GIS objects (DRAFT)

Introduction
Construction functions
Primitive functions
Spatial Predicate
Spatial Analysis
Spatial Aggregates

Introduction

To support standard GIS objects in AsterixDB, you need to use the geometry data type as follows.

DROP dataverse GeoJSON if exists;
CREATE  dataverse GeoJSON;

USE GeoJSON;

CREATE TYPE GeometryType AS{
  id : int,
  myGeometry : geometry
};

CREATE DATASET Geometries (GeometryType) PRIMARY KEY id;

Please note that even though the SRID input is supported for certain functions and is represented internally in the correct manner the serialized result (printed in the output) displays the SRID as 4326 always because of the limitations in Esri API.

Construction functions

The Geometry datatype can be created by the constructor functions.

st_make_point

Creates a 2D,3DZ or 4D point geometry.
Example:
Create a 2D point at coordinates (x,y) = (-71, 42)
Command:
```
st_make_point(-71, 42);
```

Result:

{"type":"Point","coordinates":[-71,42],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

Example:
Create a 3D point at coordinates (x,y,z) = (1,2,1.59)
Command:
```
st_make_point(1,2,1.59);
```

Result:

{"type":"Point","coordinates":[1,2,1.59],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_geom_from_text

Return a specified ST_Geometry value from Well-Known Text representation (WKT).
Example:
Create a LineString geometry from the WKT format.

Command:

st_geom_from_text("LINESTRING(1 2,3 4,5 6)");

Result:

{"type":"LineString","coordinates":[[1,2],[3,4],[5,6]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

Example:
Create a MultiLineString geometry from the WKT format.

Command:

st_geom_from_text('MULTILINESTRING((1 2,3 4,5 6),(7 8,9 10))');

Result:

{"type":"MultiLineString","coordinates":[[[1,2],[3,4],[5,6]],[[7,8],[9,10]]],"crs":null}

st_geom_from_wkb

Creates a geometry instance from a Well-Known Binary geometry representation (WKB) and optional SRID.
Example:

Command:

st_geom_from_wkb(hex("010100000000000000000000400000000000001440"));

Result:

{"type":"Point","coordinates":[2,5],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_geom_from_geojson

Creates a geometry instance from its GeoJSON representation
Example:

Command:

st_geom_from_geojson({"type":"Point","coordinates":[2,5],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}});

Result:

{"type":"Point","coordinates":[2,5],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_make_envelope

Creates a rectangular Polygon formed from the given minimums and maximums. Input values must be in SRS specified by the SRID.
Example:

Command:

st_make_envelope(10, 10, 11, 11, 4326);

Result:

{"type":"Polygon","coordinates":[[[10,10],[11,10],[11,11],[10,11],[10,10]]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

Primitive functions

There are primitive functions that take as input geometry/es and return a primitive type.

st_area

Return the area of the surface if it is a Polygon or MultiPolygon. For geometry, a 2D Cartesian area is determined with units specified by the SRID. For geography, area is determined on a curved surface with units in square meters.
Example:

Command:

st_area(st_geom_from_text('POLYGON((7 2,4 9,3 6,2.6 7,8 16))'));

Result:
```
26.500000000000007
```

st_coord_dim

Return the coordinate dimension of the Geometry value.
Example:
Command:
```
st_coord_dim(st_make_point(1,2));
```
Result:
```
2
```

st_dimension

Return the inherent dimension of this Geometry object, which must be less than or equal to the coordinate dimension.
Example:

Command:

st_dimension(st_geom_from_text('GEOMETRYCOLLECTION(LINESTRING(1 1,0 0),POINT(0 0))'));

Result:
```
1
```

geometry_type

Return the type of the geometry as a string. Eg: ‘LINESTRING’, ‘POLYGON’, ‘MULTIPOINT’, etc.
Example:

Command:

geometry_type(st_geom_from_text('LINESTRING(77.29 29.07,77.42 29.26,77.27 29.31,77.29 29.07)'));

Result:
```
"LineString"
```

st_m

Return the M coordinate of the point, or NULL if not available. Input must be a point.
Example:
Command:
```
st_m(st_make_point(1, 2, 3, 4));
```
Result:
```
4.0
```

st_n_points

Return the number of points (vertexes) in a geometry.
Example:

Command:

st_n_points(st_geom_from_text('LINESTRING(77.29 29.07,77.42 29.26,77.27 29.31,77.29 29.07)'));

Result:
```
4
```

st_n_rings

If the geometry is a polygon or multi-polygon return the number of rings.
Example:

Command:

st_n_rings(st_geom_from_text('POLYGON((10.689 -25.092, 34.595 -20.170, 38.814 -35.639, 13.502 -39.155, 10.689 -25.092))'));

Result:
```
1
```

st_num_geometries

If geometry is a GEOMETRYCOLLECTION (or MULTI*) return the number of geometries, for single geometries will return 1, otherwise return NULL.
Example:

Command:

st_num_geometries(st_geom_from_text('LINESTRING(77.29 29.07,77.42 29.26,77.27 29.31,77.29 29.07)'));

Result:
```
1
```
Example:

Command:

st_num_geometries(st_geom_from_text('GEOMETRYCOLLECTION(MULTIPOINT(-2 3 , -2 2), LINESTRING(5 5 ,10 10), POLYGON((-7 4.2,-7.1 5,-7.1 4.3,-7 4.2)))'));

Result:
```
3
```

st_num_interiorRings

Return the number of interior rings of a polygon geometry.
Example:

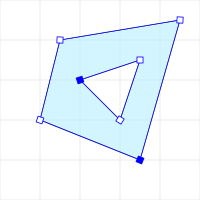Image of interiorRings * Command:

    st_num_interior_rings(st_geom_from_text("POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10),(20 30, 35 35, 30 20, 20 30))"));

Result:
```
1
```

st_x

Return the X coordinate of the point, or NULL if not available. Input must be a point.
Example:
Command:
```
st_x(st_make_point(1, 2, 3, 4));
```
Result:
```
1.0
```

st_y

Return the Y coordinate of the point, or NULL if not available. Input must be a point.
Example:
Command:
```
st_y(st_make_point(1, 2, 3, 4));
```
Result:
```
1.0
```

st_x_max

Return X maximum of a bounding box 2d or 3d or a geometry.
Example:

Command:

st_x_max(st_geom_from_text('POLYGON((10.689 -25.092, 34.595 -20.170, 38.814 -35.639, 13.502 -39.155, 10.689 -25.092))'));

Result:
```
38.814
```

st_x_min

Return X minimum of a bounding box 2d or 3d or a geometry.

st_y_max

Return Y maximum of a bounding box 2d or 3d or a geometry.

st_y_min

Return Y minimum of a bounding box 2d or 3d or a geometry.

st_z

Return the Z coordinate of the point, or NULL if not available. Input must be a point.

st_z_max

Return Z maximum of a bounding box 2d or 3d or a geometry.

st_z_min

Return Z minimum of a bounding box 2d or 3d or a geometry.

st_as_binary

Return the Well-Known Binary (WKB) representation of the geometry/geography without SRID meta data.
Example:

Command:

st_as_binary(st_geom_from_geojson({"type":"Point","coordinates":[2,5],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}));

Result:

"010100000000000000000000400000000000001440"

st_as_geojson

Return the geometry as a GeoJSON element.
Example:

Command:

st_as_geojson(st_geom_from_text('POLYGON((10.689 -25.092, 34.595 -20.170, 38.814 -35.639, 13.502 -39.155, 10.689 -25.092))'));

Result:

"{\"type\":\"Polygon\",\"coordinates\":[[[10.689,-25.092],[13.502,-39.155],[38.814,-35.639],[34.595,-20.17],[10.689,-25.092]]],\"crs\":{\"type\":\"name\",\"properties\":{\"name\":\"EPSG:4326\"}}}"

st_distance

For geometry type Return the 2D Cartesian distance between two geometries in projected units (based on spatial ref). For geography type defaults to return minimum geodesic distance between two geographies in meters.
Example:

Command:

st_distance(st_geom_from_text('POINT(-72.1235 42.3521)'),st_geom_from_text('LINESTRING(-72.1260 42.45, -72.123 42.1546)'));

Result:
```
0.0015056772638282166
```

st_length

Return the 2D length of the geometry if it is a LineString or MultiLineString. geometry are in units of spatial reference and geography are in meters (default spheroid).
Example:

Command:

st_length(st_geom_from_text('LINESTRING(-72.1260 42.45, -72.1240 42.45666, -72.123 42.1546)'));

Result:
```
0.30901547439030225
```

Spatial Predicate

Spatial predicate functions test for a relationship between two geometries and return a Boolean value (true/false).

st_intersects

Return TRUE if the Geometries/Geography “spatially intersect in 2D”.
Example:

Command:

st_intersects(st_geom_from_text('POINT(0 0)'), st_geom_from_text('LINESTRING ( 0 0, 0 2 )'));

Result:
```
true
```

st_isclosed

Return TRUE if the LINESTRING’s start and end points are coincident.
Example:

Command:

st_is_closed(st_geom_from_text('LINESTRING(0 0, 0 1, 1 1, 0 0)'));

Result:
```
true
```

st_iscollection

Return TRUE if the argument is a collection (MULTI*, GEOMETRYCOLLECTION, …)
Example:

Command:

st_is_collection(st_geom_from_text('MULTIPOINT EMPTY'));

Result:
```
true
```

st_is_empty

Return true if this Geometry is an empty geometrycollection, polygon, point etc.
Example:

Command:

st_is_empty(st_geom_from_text('POLYGON EMPTY'));

Result:
```
true
```

st_is_ring

Return TRUE if this LINESTRING is both closed and simple.
Example:

Command:

st_is_ring(st_geom_from_text('LINESTRING(0 0, 0 1, 1 1, 1 0, 0 0)'));

Result:
```
true
```

st_is_simple

Return (TRUE) if this Geometry has no anomalous geometric points, such as self intersection or self tangency.
Example:

Command:

st_is_simple(st_geom_from_text('LINESTRING(1 1,2 2,2 3.5,1 3,1 2,2 1)'));

Result:
```
false
```

st_contains

Return true if and only if no points of B lie in the exterior of A, and at least one point of the interior of B lies in the interior of A.
Example:

Command:

st_contains(st_geom_from_text('LINESTRING(1 1,-1 -1,2 3.5,1 3,1 2,2 1)'), st_make_point(-1, -1));

Result:
```
true
```

st_crosses

Return TRUE if the supplied geometries have some, but not all, interior points in common.
Example:

Command:

st_crosses(st_geom_from_text('LINESTRING(1 1,2 2,3 3,4 4, 5 5,6 6)'), st_geom_from_text('LINESTRING(0 2,1 2,2 2,3 2,4 2,5 2)'));

Result:
```
true
```

st_disjoint

Return TRUE if the Geometries do not “spatially intersect” - if they do not share any space together.
Example:

Command:

st_disjoint(st_geom_from_text('LINESTRING(1 1,2 2,3 3,4 4, 5 5,6 6)'), st_geom_from_text('POINT(0 0)'));

Result:
```
true
```

st_equals

Return true if the given geometries represent the same geometry. Directionality is ignored.
Example:

Command:

st_equals(st_geom_from_text('LINESTRING(0 0, 10 10)'), st_geom_from_text('LINESTRING(0 0, 5 5, 10 10)'));

Result:
```
true
```

st_overlaps

Return TRUE if the Geometries share space, are of the same dimension, but are not completely contained by each other.
Example:

Command:

st_overlaps(st_geom_from_text('LINESTRING(1 1,2 2,3 3,4 4, 5 5,6 6)'), st_geom_from_text('LINESTRING(0 2,1 2,2 2,3 3,4 2,5 2)'));

Result:
```
true
```

st_relate

Return true if this Geometry is spatially related to anotherGeometry, by testing for intersections between the Interior, Boundary and Exterior of the two geometries as specified by the values in the intersectionMatrixPattern.
Example:

Command:

st_relate(st_geom_from_text('LINESTRING(1 2, 3 4)'), st_geom_from_text('LINESTRING(5 6, 7 8)'), "FF1FF0102");

Result:
```
true
```

st_touches

Return TRUE if the geometries have at least one point in common, but their interiors do not intersect.
Example:

Command:

st_touches(st_geom_from_text('LINESTRING(0 0, 1 1, 0 2)'), st_geom_from_text('POINT(0 2)'));

Result:
```
true
```

st_within

Return true if the geometry A is completely inside geometry B.

Spatial Analysis

Spatial analysis functions take as input one or more geometries and return a geometry as output.

st_union

Return a geometry that represents the point set union of the Geometries.
Example:

Command:

st_union(st_geom_from_text('LINESTRING(0 0, 1 1, 0 2)'), st_geom_from_text('POINT(0 2)'));

Result:

{"type":"LineString","coordinates":[[0,0],[1,1],[0,2]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_boundary

Return the closure of the combinatorial boundary of this Geometry.
Example:

Command:

st_boundary(st_geom_from_text('POLYGON((1 1,0 0, -1 1, 1 1))'));

Result:

{"type":"MultiLineString","coordinates":[[[1,1],[-1,1],[0,0],[1,1]]],"crs":null}

st_end_point

Return the last point of a LINESTRING or CIRCULARLINESTRING geometry as a POINT.
Example:

Command:

st_end_point(st_geom_from_text('LINESTRING(1 1, 2 2, 3 3)'));

Result:

{"type":"Point","coordinates":[3,3],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_envelope

Return a geometry representing the double precision (float8) bounding box of the supplied geometry.
Example:

Command:

st_envelope(st_geom_from_text('LINESTRING(1 1, 2 2, 3 3)'));

Result:

{"type":"Polygon","coordinates":[[[1,1],[3,1],[3,3],[1,3],[1,1]]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_exterior_ring

Return a line string representing the exterior ring of the POLYGON geometry. Return NULL if the geometry is not a polygon. Will not work with MULTIPOLYGON.
Example:

Command:

st_exterior_ring(st_geom_from_text("POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10),(20 30, 35 35, 30 20, 20 30))"));

Result:

{"type":"LineString","coordinates":[[35,10],[45,45],[15,40],[10,20],[35,10]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_geometry_n

Return the 1-based Nth geometry if the geometry is a GEOMETRYCOLLECTION, (MULTI)POINT, (MULTI)LINESTRING, MULTICURVE or (MULTI)POLYGON, POLYHEDRALSURFACE. Otherwise, return NULL.
Example:

Command:

st_geometry_n(st_geom_from_text('GEOMETRYCOLLECTION(MULTIPOINT(-2 3 , -2 2),LINESTRING(5 5 ,10 10),POLYGON((-7 4.2,-7.1 5,-7.1 4.3,-7 4.2)))'),2);

Result:

{"type":"Polygon","coordinates":[[[-7,4.2],[-7.1,5],[-7.1,4.3],[-7,4.2]]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_interior_ring_n

Return the Nth interior linestring ring of the polygon geometry. Return NULL if the geometry is not a polygon or the given N is out of range.
Example:

Command:

st_interior_ring_n(st_geom_from_text("POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10),(20 30, 35 35, 30 20, 20 30))"), 0);

Result:

{"type":"LineString","coordinates":[[20,30],[35,35],[30,20],[20,30]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_point_n

Return the Nth point in the first LineString or circular LineString in the geometry. Negative values are counted backwards from the end of the LineString. Return NULL if there is no linestring in the geometry.
Example:

Command:

st_point_n(st_geom_from_text("LINESTRING(1 1, 2 2, 3 3)"), 1);

Result:

{"type":"Point","coordinates":[2,2],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_start_point

Return the first point of a LINESTRING geometry as a POINT.
Example:

Command:

st_start_point(st_geom_from_text("LINESTRING(1 1, 2 2, 3 3)"));

Result:

{"type":"Point","coordinates":[1,1],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_difference

Return a geometry that represents that part of geometry A that does not intersect with geometry B.
Example:

Command:

st_difference(st_geom_from_text("LINESTRING(1 1, 2 2, 3 3)"), st_geom_from_text("POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10),(20 30, 35 35, 30 20, 20 30))"));

Result:

{"type":"LineString","coordinates":[[1,1],[2,2],[3,3]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_intersection

Return a geometry that represents the shared portion of geomA and geomB.
Example:

Command:

st_intersection(st_geom_from_text("LINESTRING(1 1,2 2,3 3,4 4, 5 5,6 6)"), st_geom_from_text("LINESTRING(0 2,1 2,2 2,3 3,4 2,5 2)"));

Result:

{"type":"LineString","coordinates":[[2,2],[3,3]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

st_sym_difference

Return a geometry that represents the portions of A and B that do not intersect. It is called a symmetric difference because ST_SymDifference(A,B) = ST_SymDifference(B,A).
Example:

Command:

st_sym_difference(st_geom_from_text("LINESTRING(1 1,2 2,3 3,4 4, 5 5,6 6)"), st_geom_from_text("LINESTRING(0 2,1 2,2 2,3 3,4 2,5 2)"));

Result:

{"type":"MultiLineString","coordinates":[[[0,2],[1,2],[2,2],[1,1]],[[5,2],[4,2],[3,3],[4,4],[5,5],[6,6]]],"crs":null}

st_polygonize

Aggregate. Creates a GeometryCollection containing possible polygons formed from the constituent linework of a set of geometries.
Example:

Command:

st_polygonize([st_geom_from_text("LINESTRING(1 1,2 2,3 3,4 4, 5 5,6 6)"), st_geom_from_text("LINESTRING(0 2,1 2,2 2,3 3,4 2,5 2)")]);

Result:

{"type":"GeometryCollection","geometries":[{"type":"LineString","coordinates":[[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]]},{"type":"LineString","coordinates":[[0,2],[1,2],[2,2],[3,3],[4,2],[5,2]]}],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

Spatial Aggregates

spatial aggregate function which takes as input a set of geometries and return one geometry as the result.

st_union

Returns a geometry that represents the point set union of the Geometries.
Example:

Command:

st_union((SELECT VALUE gbu FROM [st_make_point(1.0,1.0),st_make_point(1.0,2.0)] as gbu));

Result:

{"type":"MultiPoint","coordinates":[[1,1],[1,2]],"crs":{"type":"name","properties":{"name":"EPSG:4326"}}}

Support the standard GIS objects (DRAFT)

Table of Contents

Introduction

Construction functions

st_make_point

st_geom_from_text

st_geom_from_wkb

st_geom_from_geojson

st_make_envelope

Primitive functions

st_area

st_coord_dim

st_dimension

geometry_type

st_m

st_n_points

st_n_rings

st_num_geometries

st_num_interiorRings

st_x

st_y

st_x_max

st_x_min

st_y_max

st_y_min

st_z

st_z_max

st_z_min

st_as_binary

st_as_geojson

st_distance

st_length

Spatial Predicate

st_intersects

st_isclosed

st_iscollection

st_is_empty

st_is_ring

st_is_simple

st_contains

st_crosses

st_disjoint

st_equals

st_overlaps

st_relate

st_touches

st_within

Spatial Analysis

st_union

st_boundary

st_end_point

st_envelope

st_exterior_ring

st_geometry_n

st_interior_ring_n

st_point_n

st_start_point

st_difference

st_intersection

st_sym_difference

st_polygonize

Spatial Aggregates

st_union